#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
int n, k;
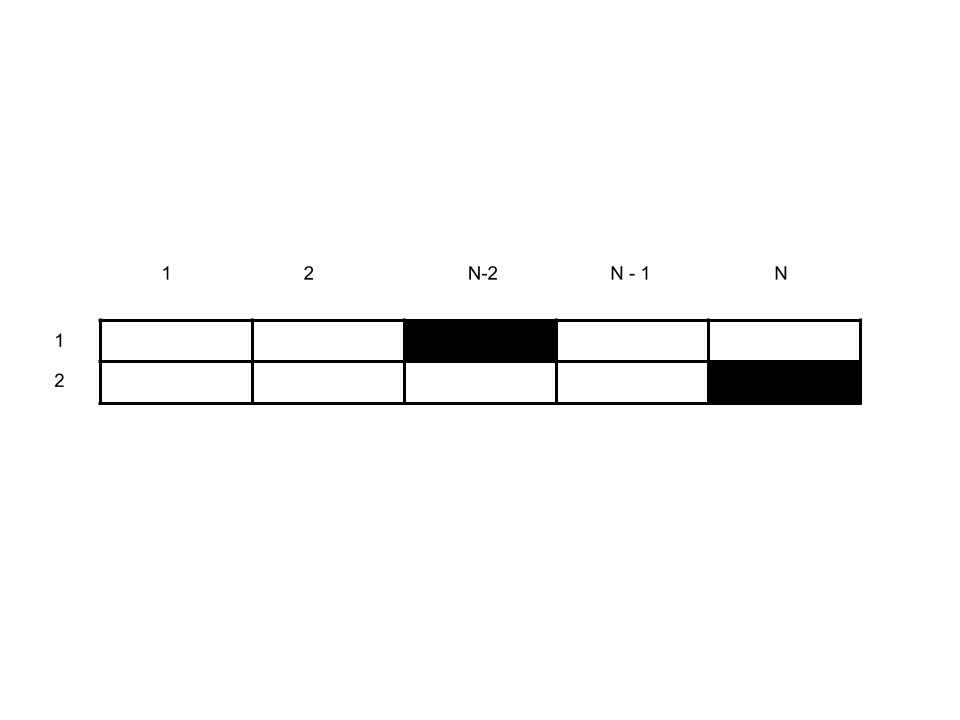
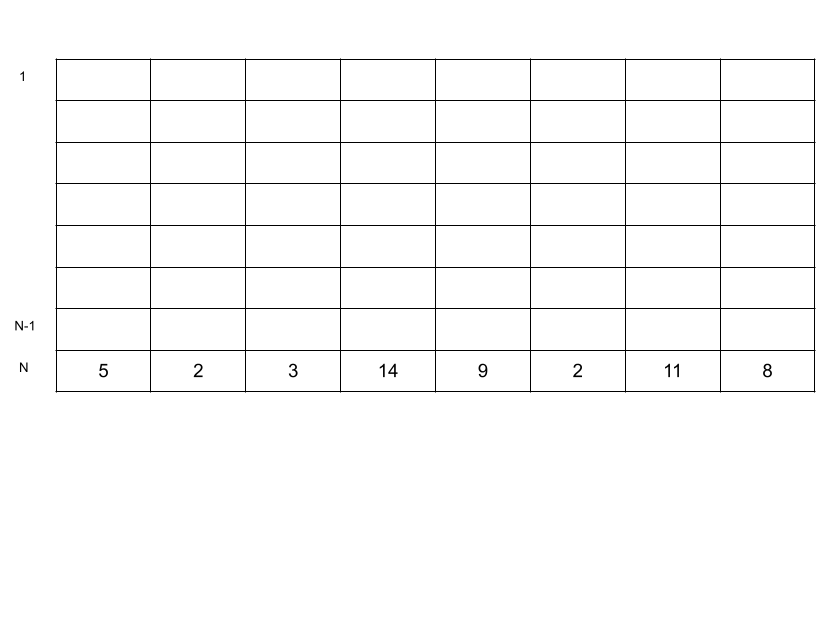
int board[101][101];
int levitation[101][101];
int tempLevitation[101][101];
int tempAdjust[101][101];
int tempArrange[101][101];
void input() {
cin >> n >> k;
for (int i = 1; i <= n; i++) {
cin >> board[n][i];
}
}
void init() {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
tempAdjust[i][j] = 0;
tempArrange[i][j] = 0;
}
}
}
// 1. 물고기의 수가 가장 적은 어항에 물고기 한 마리 넣는다.
// 여러개라면 모두에 한 마리씩 넣는다.
void putFish() {
vector<int> temp;
int minValue = 1e9;
for (int i = 1; i <= n; i++) {
if (board[n][i] < minValue) {
minValue = board[n][i];
temp = {};
temp.push_back(i);
}
else if (board[n][i] == minValue) {
temp.push_back(i);
}
}
for (auto index : temp) {
board[n][index]++; // 물고기를 한 마리씩 넣는다.
}
}
// 2. 어항을 쌓는다.
void rotate() {
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
tempLevitation[i][j] = levitation[i][j];
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
levitation[j][n - i] = tempLevitation[i][j];;
}
}
}
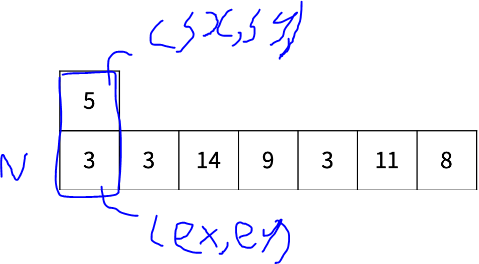
void pile() {
// 먼저, 가장 왼쪽에 있는 어항을 그 오른쪽에 있는 어항의 위에 올려 놓는다.
board[n - 1][1] = board[n][1];
for (int i = 2; i <= n; i++) {
board[n][i - 1] = board[n][i]; // N행을 왼쪽으로 한 칸씩 이동
board[n][i] = 0;
}
// 2개 이상 쌓여있는 어항을 공중부양 시킨다.
int sx = 1, sy = 1, ex = n, ey = 1;
while (true) {
for (int i = n; i >= 1; i--) {
if (board[i][1] == 0) {
sx = i + 1;
break;
}
}
for (int i = 1; i <= n; i++) {
if (board[sx][i] == 0) {
ey = i - 1;
break;
}
}
int bottomCnt = 0;
for (int i = ey + 1; i <= n; i++) {
if (board[n][i]) {
bottomCnt++;
}
else {
break;
}
}
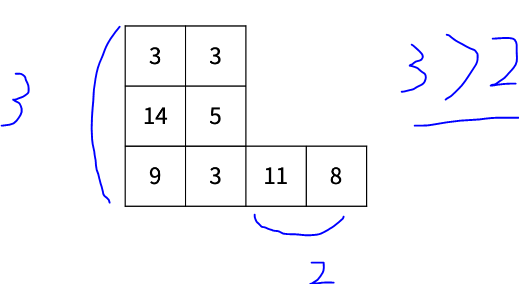
if (ex - sx + 1 > bottomCnt) break; // 공중 부양 시킨 배열의 세로 길이가 맨 바닥의 길이보다 크면 더 이상 회전 X
fill(&levitation[0][0], &levitation[100][101], 0);
for (int i = sx; i <= ex; i++) {
for (int j = sy; j <= ey; j++) {
levitation[i - sx + 1][j - sy + 1] = board[i][j];
}
}
// 배열의 맨 밑바닥을 맨 왼쪽으로 밀어 넣는다.
int col = 1;
for (int i = ey + 1; i <= n; i++) {
if (board[n][i]) {
board[n][col] = board[n][i];
board[n][i] = 0;
col++;
}
}
rotate(); // 공중 부양 배열을 90도 회전시킨다.
int row = n - 1; // 회전시킨 공중 부양 배열을 한 칸 위에 쌓는다.
col = 1;
for (int i = n; i >= 1; i--) {
for (int j = 1; j <= n; j++) {
if (levitation[i][j]) {
board[row][col] = levitation[i][j];
col++;
}
}
if (col > 1) {
col = 1;
row--;
}
}
}
}
// 3. 어항에 있는 물고기의 수를 조절한다.
bool check(int x, int y) {
return !(x < 1 || y < 1 || x > n || y > n || board[x][y] == 0);
}
void adjust() {
init();
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
if (board[i][j] == 0) continue;
if (check(i + 1, j)) {
int d = abs(board[i][j] - board[i + 1][j]) / 5;
if (d > 0 && board[i][j] > board[i + 1][j]) {
tempAdjust[i][j] -= d;
tempAdjust[i + 1][j] += d;
}
else if (d > 0 && board[i][j] < board[i + 1][j]) {
tempAdjust[i][j] += d;
tempAdjust[i + 1][j] -= d;
}
}
if (check(i, j + 1)) {
int d = abs(board[i][j] - board[i][j + 1]) / 5;
if (d > 0 && board[i][j] > board[i][j + 1]) {
tempAdjust[i][j] -= d;
tempAdjust[i][j + 1] += d;
}
else if (d > 0 && board[i][j] < board[i][j + 1]) {
tempAdjust[i][j] += d;
tempAdjust[i][j + 1] -= d;
}
}
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
board[i][j] += tempAdjust[i][j];
if (board[i][j] < 0) board[i][j] = 0;
}
}
}
// 4. 이제 다시 어항을 바닥에 일렬로 놓는다.
void arrange() {
int col = 1;
init();
for (int j = 1; j <= n; j++) {
for (int i = n; i >= 1; i--) {
if (board[i][j] == 0) continue;
tempArrange[n][col] = board[i][j];
col++;
}
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= n; j++) {
board[i][j] = tempArrange[i][j];
}
}
}
// 5. 새로운 공중 부양
void pile2() {
int sx = n, sy = 1, ex = n, ey = n / 2;
fill(&levitation[0][0], &levitation[100][101], 0);
for (int i = sx; i <= ex; i++) {
for (int j = sy; j <= ey; j++) {
levitation[i - sx + 1][j - sy + 1] = board[i][j];
}
}
int col = 1;
for (int i = ey + 1; i <= n; i++) {
if (board[n][i]) {
board[n][col] = board[n][i];
board[n][i] = 0;
col++;
}
}
rotate();
rotate();
int row = n - 1;
col = 1;
for (int i = n; i >= 1; i--) {
for (int j = 1; j <= n; j++) {
if (levitation[i][j]) {
board[row][col] = levitation[i][j];
col++;
}
}
if (col > 1) {
col = 1;
row--;
}
}
}
void pile3() {
int sx = n - 1, sy = 1, ex = n, ey = n / 4;
fill(&levitation[0][0], &levitation[100][101], 0);
for (int i = sx; i <= ex; i++) {
for (int j = sy; j <= ey; j++) {
levitation[i - sx + 1][j - sy + 1] = board[i][j];
}
}
int col = 1;
for (int i = ey + 1; i <= n; i++) {
if (board[n][i]) {
board[n][col] = board[n][i];
board[n][i] = 0;
col++;
}
}
col = 1;
for (int i = ey + 1; i <= n; i++) {
if (board[n - 1][i]) {
board[n - 1][col] = board[n - 1][i];
board[n - 1][i] = 0;
col++;
}
}
rotate();
rotate();
int row = n - 2;
col = 1;
for (int i = n; i >= 1; i--) {
for (int j = 1; j <= n; j++) {
if (levitation[i][j]) {
board[row][col] = levitation[i][j];
col++;
}
}
if (col > 1) {
col = 1;
row--;
}
}
}
void solve() {
init();
input();
int ans = 0;
while (*max_element(board[n] + 1, board[n] + n + 1) - *min_element(board[n] + 1, board[n] + n + 1) > k) {
putFish();
pile();
adjust();
arrange();
pile2();
pile3();
adjust();
arrange();
ans++;
}
cout << ans;
}
int main() {
ios_base::sync_with_stdio(false);
cin.tie(NULL); cout.tie(NULL);
solve();
return 0;
}